Если вы хотите посетить официальный сайт казино, вам потребуется выполнить несколько простых шагов.
Первым шагом является открытие веб-браузера и ввод в поисковую строку ключевого слова «Вавада казино». После этого нажмите «Enter» или «Поиск». Вы должны обратить внимание, что официальный сайт Vavada казино будет включать ключевые слова из заголовка, такие как «официальный сайт» и «Вавада казино».
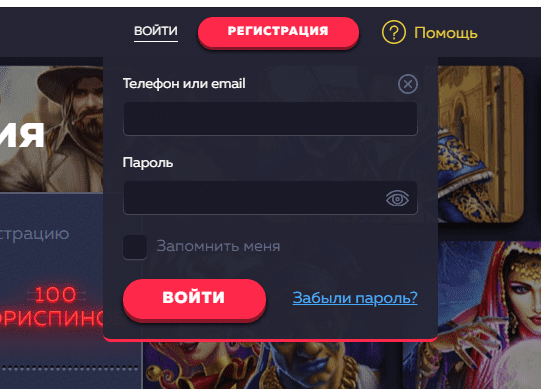
Если у вас уже есть учетная запись в Vavada casino, вам нужно будет нажать на раздел «Вход». После этого вы должны ввести свои учетные данные, такие как имя пользователя и пароль, и нажать кнопку «Войти».
Рабочее зеркало Вавада
Рабочее зеркало Vavada, — это сайт, предоставляющий альтернативную точку доступа к онлайн-казино Vavada. Из-за государственных ограничений или блокировок официальный сайт может быть недоступен в некоторых регионах. В таких случаях рабочее зеркало Вавада предлагает решение, обходя эти ограничения и позволяя пользователям продолжать пользоваться платформой.
Чтобы найти рабочее зеркало Вавада, пользователи могут воспользоваться поиском в Интернете по определенным ключевым словам или фразам, например «рабочее зеркало Вавада» или «ссылка на зеркало Vavada». Такой поиск выдаст несколько результатов с перечислением доступных зеркал. Кроме того, Vavada может отправлять уведомления зарегистрированным пользователям, информируя их о последней ссылке на рабочее зеркало.
Вавада регистрация: 2 важных правила для новичков
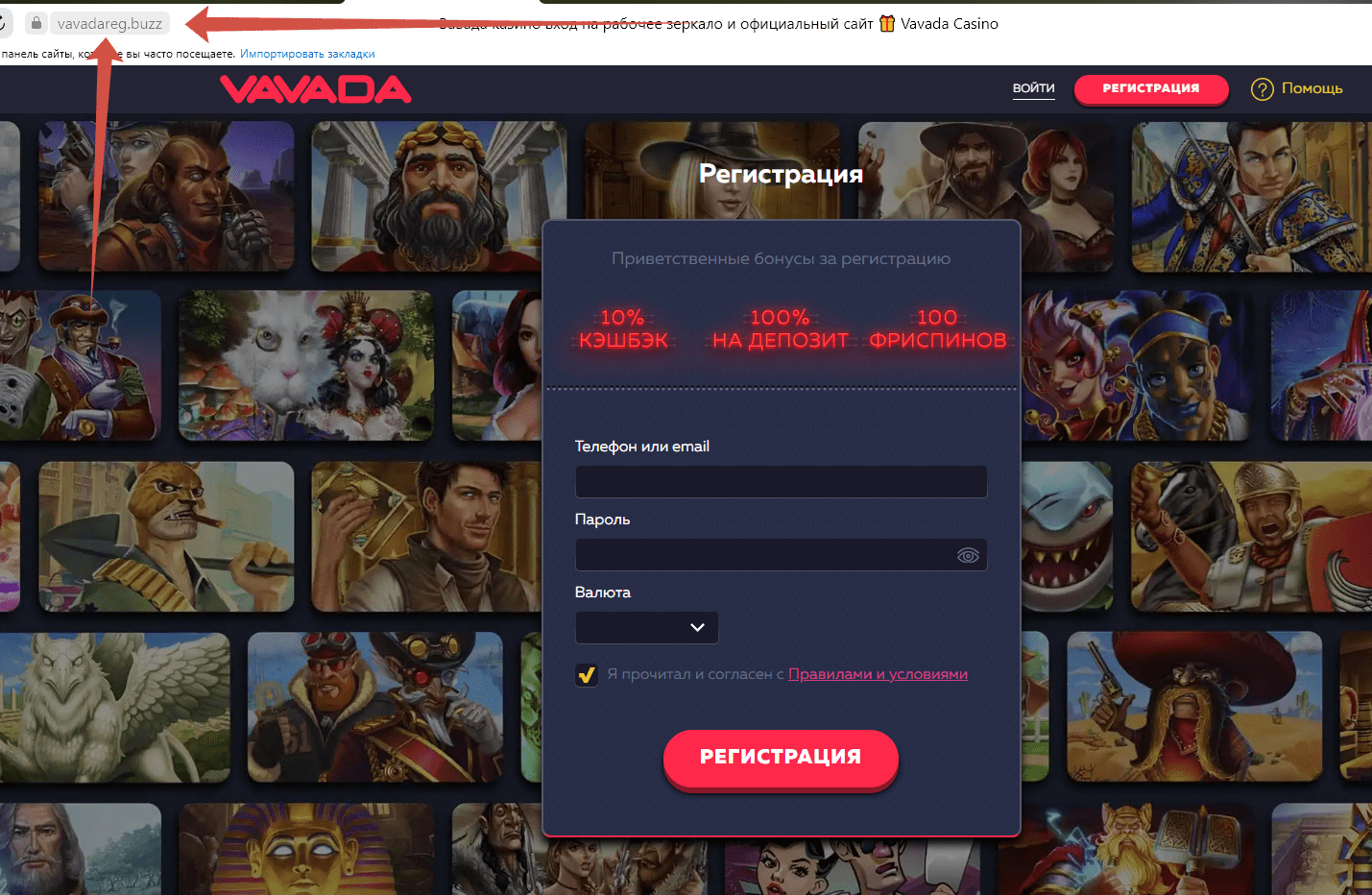
Для успешной регистрации на официальном сайте казино Вавада необходимо следовать нескольким простым действиям. В первую очередь, потенциальный новичок должен посетить официальный сайт Вавада и найти раздел «Регистрация» или «Создать аккаунт». Обычно данный раздел располагается в верхней части страницы.
После этого потребуется заполнить регистрационную форму, предоставляя следующую информацию: имя и фамилию пользователя, электронную почту для связи, пароль для входа на сайт, валюту для игрового счета, а также подтвердить согласие с правилами и условиями использования сайта.
Вавада бонусы на сегодня
Вавада – это онлайн-казино, которое предлагает широкий выбор игр и специальных бонусов для своих клиентов. Бонусы на сегодня считаются чрезвычайно важным инструментом для привлечения и удержания игроков, и Вавада предлагает разнообразные поощрения, чтобы удовлетворить потребности различных категорий клиентов. В этой статье мы рассмотрим, какие бонусы доступны сегодня в Вавада казино, и как их получить. Если вы являетесь поклонником азартных игр и стремитесь увеличить свои шансы на выигрыш, то тщательно изучите эту информацию, чтобы получить максимальную выгоду от игры в Вавада. От регистрации до участия в акциях, у Vavada casino есть много возможностей получить дополнительные бонусы, чтобы улучшить ваш опыт игры и увеличить шансы на успех.
Вавада бездепозитный бонус
Вавада бездепозитный бонус за регистрацию — это привлекательное предложение от онлайн-казино Вавада, предоставляющее новым игрокам возможность получить бесплатные средства для игры без необходимости внесения депозита. Для получения данного бонуса необходимо пройти процедуру регистрации на официальном сайте казино.
Условия использования бонуса бездепозитного в Вавада казино могут включать указание промо-кода или автоматическую активацию бонуса после создания аккаунта. Также могут быть установлены некоторые ограничения, например, максимальная сумма, которую можно выиграть с помощью данного бонуса, и требование выполнить определенный оборот на игровых автоматах или других играх, прежде чем вы сможете вывести свои выигрыши.

Мобильное приложение Вавада
Мобильное приложение Вавада это игровая платформа, доступная исключительно на устройствах с операционной системой Андроид. Установку приложения Vavada casino можно осуществить только через официальный сайт Вавада, где можно найти специальную ссылку для скачивания. Одно из главных преимуществ приложения — его небольшой размер, всего 32 мегабайта, что позволяет сэкономить место на мобильном устройстве.










































